Speaker
Description
$\quad$ Based on fundamental studies [1,2], a phenomenological model was proposed [3], which takes into account Coriolis mixing of the ground (gr), $\beta$ -, $\gamma$ - vibrational, and $K^\pi=1^+$ bands. It was shown that the mixing effect is strongly manifested in the energy levels of the $\beta$ - and $\gamma$ - band and leads to significant deviations from the adiabatic theory of interband transitions from the $\beta$ - and $\gamma$ - band levels.
$\quad$ Deviations from the adiabatic theory in the energies of the ground-state band are observed at high spins, which is associated with its mixing with other rotational bands. In the first-order approximation of perturbation theory, the Coriolis force mixes the states of the ground band with levels of bands that possess specific quantum characteristics. To date, such states have been experimentally identified in many even-even nuclei, with excitation energies of approximately $E_1 \approx 2.5$ MeV.
$\quad$ In this work, to study the moment of inertia and the energy levels of the ground rotational band, we use the two-parameter Harris formula [2] and a phenomenological model [3], taking into account only the Coriolis mixing between the ground band and experimentally known bands. This model framework provides a more accurate description of the rotational energy spectrum of the ground band beyond the rigid rotor approximation.
$\quad$ Calculations were performed for even isotopes of $^{222-232}\rm{Th}$, $^{232}\rm{U}$, $^{236-246}\rm{Pu}$, $^{242-248}\rm{Cm}$, $^{248-250}\rm{Fm}$, and $^{252-254}\rm{No}$. Theoretical predictions are systematically compared with available experimental data and with the results of previous models [4,5]. The comparison, presented in Figure 1, shows that the theoretical values obtained from our model are in good agreement with experimental results, especially regarding the effective moment of inertia. This agreement confirms the validity and reliability of the proposed model in describing the collective behaviour of the nuclei under study.
$\quad$ In the future, this work can be extended by including additional interaction terms or by applying the approach to a broader range of isotopes.
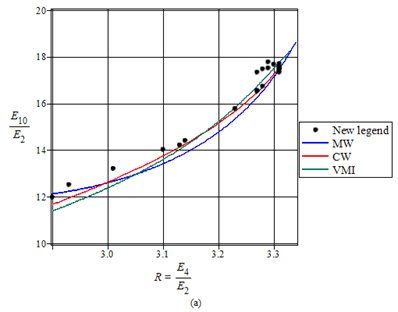
Fig. 1, the ratio E10/E2 as a function of E4/E2. It shows the comparison between the current work (CW), the variable moment of inertia VMI (Mariscotti et. al. 1969), the work in ref. [5] and the experimental work.
- Bohr A. and Mottelson B.R. 1997. Nuclear Structure. vol. 1,2 (NewYork:Benjamin)
- Harris S.M., Phys. Rev. 138, B509 (1965).
- Usmanov, P.N., Okhunov, A. A., Salikhbaev, U.S. and Vdovin, A.I. Phys. Part. Nucl. Lett. 7, 185 (2010).
- Usmanov, P. N., Okhunov, A. A., & Abu El Sheikh, M. Kh. M. (2022). The effect of the quantization of the centrifugal stretching on the analysis of the rotational spectra of even-even nuclei. Sains Malaysiana, 51(4), 1213–1227.
- Mariscotti, M.A.J., Scharff-Goldhaber, G. & Buck, B. 1969. Phenomenological analysis of ground state bands in even-even nuclei. Physical Review 178(4): 1864-1887.
- https://doi.org/10.17576/jsm-2022-5104-21

